Задания к игре “Уникуб”

Задания к игре Уникуб

Скачать и распечатать
60 заданий к интеллектуальной игре “Уникуб” из книги Никитина.
Рисунки и тексты

Как сделать “Уникуб” своими руками >>>

Игра “Уникуб” (Система Никитиных)

Купить >>

Лучшая из игр для развития математических способностей поможет в усвоении арифметики, алгебры и геометрии.
Игра помогает овладеть графической грамотностью, понимать еже до школы план, карту, чертеж.

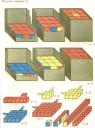
Задания к игре “Уникуб”

У-1. Сложи кубики в коробку. С самыми маленькими (1,5 - 3 года) лучше начинать с укладки кубиков в коробку. “Давай сложим так, чтобы всё донышко в коробке было красным!” - и, конечно, обрадоваться, что получилось хорошо. Огорчает малышей только кубик без красных граней. Его можно уложить последним в середине, чтобы было похоже на фонарик.

У-2. Кто сумеет сложить кубики так, чтобы донышко было синим, серединка - жёлтой, а верх - красным? Малышу можно показать рисунок в книге.

У-3. Красный поезд. Нужно сложить из кубиков поезд, как показано на рисунке. Крыши, стены вагонов и электровоз — красные (с тех сторон, которые видны на рисунке). Положите, а лучше поставьте или повесьте вертикально перед малышом рисунок У-1. Длина поезда может быть и точно такая, как на рисунке, и больше. Это зависит от настроения “машиниста”. Главная трудность задания для малыша — одновременно следить за двумя плоскостями и к тому же отбирать подходящие кубики (с 2 и 3 красными гранями). Если он раньше выполнял задание “Сложи узор”, задание для него будет сравнительно легким. Но если он сделает красными только крыши вагонов, а стенки получатся не у всех вагонов красными — похвалите его.

– Хорошо маляры покрасили крыши — все красные. А теперь посмотрим, как маляры покрасили стенки.
И “идите” указательным и средним пальцами вдоль поезда. Остановитесь около вагона со стенкой другого цвета и подумайте: “Посылать ли вагон в перекраску или нет?” Решение должен принять сам “машинист”.

У-4. Желтая квадратная коробка. Малыш должен решить, какие кубики надо взять, чтобы и 4 боковые грани были желтыми? Варианты — синяя и красная коробки.

У-5. Кто сложит квадратную площадку из 9 кубиков. Это игровая площадка для дошкольников. Все 4 боковые ее грани желтые.

У-6. Синяя квадратная площадка из 16 кубиков. Это может быть спортплощадка для школьников. Все грани, кроме нижней, — синие.

У-7. Красная квадратная площадка из 25 кубиков - это сцена для летнего театра. Здесь уже надо различать, какие “сорта” кубиков надо укладывать по периметру и какие в центр модели, иначе может не хватить кубиков нужного цвета.

У-8. Классификация по красным. Разложите кубики по “сортам” или лучше сделать “три поезда”. В первом поезде все вагоны с одной красной крышей, во втором - с красными крышами и одной красной стенкой, в третьем - с красной крышей и двумя красными стенками. Получаются три “состава” разной длины и один “тепловоз” (кубик без красных граней).

С классификации начинается серьезное овладение “Уникубом”, поэтому ее можно дать значительно раньше, т. е. после выполнения первых трех заданий, особенно в том случае, если малыш уже считает до 3 — 5 и может различать “сорта” кубиков. Мы не придумали названия каждому “сорту” кубиков и пользуемся плодами детского словотворчества: “однушка красная”, “двушка синяя”, “трешка желтая” и “нулевка”. В таком названии ясно видно, по какому цвету шла классификация и сколько граней этого цвета есть на кубике. Малышей такая терминология устраивает, и, складывая квадратную сцену для летнего театра (У-6), они сразу говорят: “По углам я поставлю “красные трешки”, между ними “красные двушки”, а в середину можно класть “красные однушки” и что останется”.
Предварительная классификация кубиков по красному, синему или желтому цвету значительно облегчает выполнение любого задания, поэтому часто малыши по собственной инициативе, перед тем как приступить к новому заданию, делают такую классификацию. При этом они уже понимают, какой цвет лучше выбрать и делать ли классификацию полностью или отобрать одни “трешки” или “двушки”.

У-9. Посчитайте, сколько вагонов в поезде, где у вагонов только красные крыши (сколько в “Уникубе” красных “однушек”). Сколько вагонов в поезде с красными крышами и одной красной стенкой? (Сколько красных “двушек”?) Сколько вагонов в третьем поезде? (Сколько красных “трешек”?) Из кубиков какого “сорта” можно сложить малый куб (из 8 кубиков) одного цвета?

У-10. Три беговые дорожки на стадионе из 9 кубиков разного цвета. Боковые грани имеют цвет прилегающей дорожки.

У-11. Кто сложит синюю букву П? Малыши могут следить только за цветом буквы, а старшим можно добавить: сложи так, чтобы стенки были такими же, как на рисунке У-11.

У-12. Красная буква Н. Так же можно складывать любые буквы, которые хорошо получаются из кубиков (Г, Е, О, С, Т, Ч и др.).

У-13. Трехцветная скамейка для электрички. К сожалению, на невидимой стороне только сиденья скамейки можно сделать того же цвета, что и на видимой, а спинки получаются другого.

У-14. Рыцарский замок с 4 башенками по углам.

У-15. Атомный ледокол с красной палубой, синими бортами и желтыми палубными надстройками.

У-16. Разноцветная крепость с бойницей.

У-17. Цирковая лесенка с синими ступенями с двух сторон. Сколько кубиков надо для такой лесенки?

У-18. Шахматная доска 5Х5 с желто-красными клетками. Четыре боковые грани тоже с шахматной окраской. Возможны варианты: красно-синяя, желто-синяя.

У-19. Египетская пирамида. Правые и левые стенки — красные, передние и задние — желтые, “крыши” всех ярусов — синие. Для пирамиды не обязательно иметь 30 кубиков, вполне достаточно 27 кубиков. Задайте малышу задачу: как построить прочную пирамиду, если 3 кубиков не хватает? Где можно сэкономить эти кубики? (Вместо 4 центральных кубиков в 1 ярусе можно поставить 1 в центре (”гробница фараона”) и повернуть его на 45 градусов, чтобы на него опирались сразу 5 кубиков 11 яруса.)

У-20. Желтое шоссе размером 3Х9 с одним красным квадратом в центре. Четыре боковые грани — желтые.

У-21. Красный пятиэтажный дом с окошками, с синими крышами на всех этажах и красными полами во всех комнатах. Задняя стена дома и стены комнат могут быть любого цвета.

У-22, 23, 24. Три водонапорные башни разной высоты. Кроме соблюдения порядка окраски здесь есть еще “секрет” технологии строительства. Без открытия этого “секрета” построить 2-ю, а особенно 3-ю башню очень трудно. Пусть малыш сам откроет этот “секрет”. (”Секрет” состоит в порядке складывания: сначала надо заготовить все этажи, но складывание надо начинать с верхнего этажа, а не с нижнего, как принято во всяком строительстве.)

У-25. Кто быстрее сложит малый куб красного цвета? Все 6 граней должны быть красными. Варианты: желтый и синий кубы. К сожалению, их нельзя сложить одновременно, а только последовательно.

У-26. Малый куб трех цветов. По 2 соседние (примыкающие) грани одинакового цвета (куб Вадика Склере, 6 лет).

У-27. Малый куб двух цветов. Три грани, образующие одну вершину, — синие, три другие — желтые. Варианты: желто-красный и красно-синий.

У-28. Малый куб трех цветов. Противоположные грани одного цвета (куб Вадика Склере, 6 лет).

У-29. Малый куб двух цветов. Нижняя, задняя и верхняя грани синего цвета, а левая, передняя и правая — красного. Варианты — иные сочетания цветов.

У-30. Синяя вокзальная скамейка. Со всех сторон она окрашена в синий цвет (кроме “дна”). Можно сложить такую же скамейку красного или желтого цвета.

У-31. Красный колодец. Снаружи он со всех сторон красный, а внутри — синий (”вода”). К сожалению, для внутренней окраски недостает одной синей грани и в колодце виден “песок” (одна желтая грань).

У-32. Кресло с подлокотниками. Обтянуто снаружи синим, а внутри и спереди красным бархатом. Цвета обивки можно менять.

У-33. Антошина скамейка. Сколько человек могут сесть на скамейку одновременно (каждый кубик — сиденье). Сиденья и спинки с одной стороны — красные, с другой — синие, а верх и торцы — желтые (скамейка Антона Никитина, 7 лет).

У-34. Счет. Почему кубиков с 1 красной гранью только 6? (По числу граней куба.) Почему кубиков с 2 красными гранями — 12? (По числу ребер куба). Почему кубиков с 3 красными гранями — 8? (По числу вершин куба.) Почему кубиков без красных граней только 1? Сколько граней у одного кубика? Кто быстрее подсчитает, сколько красных граней на всех кубиках? Сколько всех граней на всех кубиках? Сколько граней у 6 кубиков, у 8 кубиков, у 12 кубиков, у 27?

У-35. Большой куб красного цвета. Проверьте, все ли 6 граней красного цвета, так как часто (особенно те, кто складывает впервые) забывают, что “дно” должно быть такого же цвета, как и остальные грани. Можно складывать большой синий и большой желтый кубы.

Это одно из самых часто повторяемых заданий и заданий, которые делают “на время”. На складывание у 3 — 4-летних уходит 10 минут, у 5 — 6-летних — до 2 минут, а 10 — 12-летние дети могут выполнить это задание даже за 1 минуту. “Рекордсмены”, работая двумя руками сразу и по определенной системе, могут “выйти из минуты”.

У- 36. Большой куб трех цветов. Две соседние грани одинакового цвета.

У-37. Большой трехцветный куб с противоположными гранями одного цвета.

У-38. Большой трехцветный куб с горизонтальными слоями одного цвета.

У-39. Двухцветный куб, 3 грани, образующие вершину, — желтого цвета, 3 другие — синего. Возможны другие сочетания цветов: желтого с красным, красного с синим.

У-40. Большой двухцветный куб. Нижняя, задняя и верхняя грани синего цвета, а левая передняя и правая — красного (куб Саши Дунаева, 6 лет). Можно использовать и другие сочетания цветов.

У-41. Высотный дом желтого цвета на 20 квартир. В основании – 4 кубика, и высота — 5 этажей. Стены, крыша и пол на 1-м этаже желтого цвета. Окраску дома можно делать и красной, и синей.

У-42. Большой куб с шахматной окраской всех 6 граней. Сочетания цветов могут быть и другие: сине-красные, желто-красные.

У-43. Кто быстрее сложит красный крест на всех 6 гранях? Вершины куба могут быть и желтыми, и синими.

У-44. Кто быстрее сложит букву П на всех 6 гранях? Цвет букв на противоположных гранях одинаков. Могут быть варианты: все буквы одного цвета (красные, желтые, синие).

У-45. Кто быстрее сложит букву Н на всех 6 гранях? Цвет букв на противоположных гранях одинаков. Придумайте другие варианты.

У-46. Сложи трехэтажный красный дом на 9 квартир, но так, чтобы задняя стенка была синей. Это может быть подготовка к разъемным заданиям, где работает “внутренний порядок”.

У-47. Большой разъемный красный куб. Все 6 наружных граней — красные, любые соприкасающиеся грани разъема — одноцветные (желтые или синие). Возможны варианты другого цвета.

Это задание решающее во многих отношениях. Во-первых, выполнив его, можно убедиться, что окраска “Уникуба” при изготовлении была безошибочной. Во-вторых, ребенок, справившийся с заданием У-47, сможет справиться и с любым другим.
Интересно, что тренировка в решении задания У-47 только в самой начальной стадии заметно улучшает результаты взрослых, а затем они изменяются мало, и взрослые вообще, как правило, не могут дойти до результатов, показываемых детьми уже в 10 — 12 лет (отстают по времени в 2 — 3 раза). Исключения здесь крайне редки.

У-48. Двойная классификация. Кубики сначала надо разложить по “сортам”, как в задании У-8, по красному цвету. Получится ряд с одной красной гранью (К-1), ряд с двумя красными гранями (К-2) и ряд с тремя красными гранями (К-3).

Затем внутри каждого ряда разложить их по сортам, но уже синего (или если надо — желтого) цвета. Ближе к себе положить кубики с тремя синими гранями, далее — с двумя и еще дальше — с одной. Получаются “триады”, как на У-43. Двойная классификация заметно облегчает выполнение сложнейших заданий N 44 — 50, так как сразу можно найти кубик с заданным числом и цветом граней. Например, все “трешки красные” лежат в ряду К-3, “трешки синие” — это ближайшие к ребенку кубики (их просто видно), а “трешки желтые” — самые дальние в каждом ряду.

У-49. Малый разъемный куб красного цвета. Любые грани разъема одного цвета (куб Антона Никитина, 8 лет). Варианты: желтый куб, синий куб.

У-50. Двухсторонняя шахматная доска, размером 5Х5 (У-46). Все 6 ее граней имеют шахматную окраску. Большая, невидимая на рисунке грань должна быть красно-желтой или желто-синей, а узкие грани — той же окраски, что и одна из широких. На рис. 46 все они красно-синие. Это одно из сложнейших заданий. При его выполнении почти все допускают ошибки и теряют массу времени на их исправление, перестановку кубиков (доска Сережи Беляева, 14 лет).

У-51. Большой красный куб. Любые соприкасающиеся грани разъема разного цвета. Внешне этот куб такой же, как У-47, но “внутреннее устройство” у него другое — соприкасающиеся грани разъема — разного цвета. Внешнюю окраску можно задавать и другого цвета (желтую или синюю), но тогда соответственно изменяется и внутренняя окраска (куб Антона Никитина, 10 лет).

У-52. Большой красный куб. Любые соприкасающиеся грани разъема — полосатые. Возможны 6 вариантов: три варианта определяются цветом внешней окраски (красный, желтый, синий), и внутри каждого из них есть по два варианта внутренней окраски по разъемам. Один, показанный на рисунке-задании, при котором соприкасаются в каждом разъеме разноцветные полосы (синие с желтыми), и второй – когда соприкасаются полосы одноцветные (куб Антона Никитина, 10 лет).

У-53. Кто сложит большой куб так, чтобы:

- во фронтальных плоскостях все наружные и внутренние грани были одноцветные (2 желтых, 2 красных, 2 синих);
- в боковых плоскостях (справа, слева и в параллельных сечениях между ними) полосатые, трехцветные (6 граней);
- в горизонтальных плоскостях (сверху, снизу и в сечениях между ними шахматной окраски, двухцветные (6 граней)? (Куб Володи и Наташи Лисун из Киева).

У-54. Большой красный куб. Все 12 соприкасающихся граней разъема имеют шахматную окраску. Здесь так же можно изменять цвет наружных граней, а соприкасающиеся грани разъема или могут быть зеркальным отражением друг друга, или соприкасаться разноцветными квадратиками, как У-50 (куб Антона Никитина, 10 лет).

У-55. Кто сложит большой куб, чтобы все наружные грани попарно противоположные были одноцветны;- все внутренние грани разъема, соприкасающиеся, попарно одноцветные? (Куб Толи Заверняева, 19 лет).

У-56. Кто сложит большой куб так, чтобы все наружные и все грани разъемов (12) образовали букву О. т.е. 6 красный, 6 желтых и 6 синих букв? (Куб Оли Никитиной, 17 лет).

У-57. Кто сложит большой куб так, чтобы по всем 18 наружным и внутренним граням были буквы Н (6 синих, 6 красных, 6 желтых)?

У-58. Кто сложит большой куб так, чтобы на его наружных гранях были красные кресты, а на внутренних гранях разъема 6 синих и 6 желтых? (Куб Вани Никитина, 10 лет)

У-59. Кто сложит большой куб так, чтобы все наружные и все внутренние грани разъема (18 граней) были полосатые трехцветные? (Куб Толи Заверняева, 19 лет).

У-60. Кто сложит большой куб наивысшей сложности? Все 6 наружных граней и 12 внутренних имеют шахматную окраску. Если снаружи 6 красно-синих, то 6 внутренних красно-желтые и еще 6 сине-желтые (Куб Антона Никитина, 19 лет).

Из книги Никитина “Развивающие игры”